X kg de abono----------------------355 m2 de superficie de terreno.X= (0,5 x 355)/10
X=17,75 kg de abono
Hoy os muestro una forma rápida y sencilla de calcular alineaciones de plantas para perimetrar zonas en forma de cuadrado o de rectángulo.
Para realizar cuadrados:
Si queremos formar cuadrados la fórmula es (Ax4)-4, siendo "A" el número de plantas por lado. Aplicamos: (4x4)-4=12, con 12 plantas formamos este cuadrado.
Imaginad ahora que queremos hacer un cuadrado de 6x6, aplicamos la fórmula: (6x4)-4=20 plantas.
Ahora para hacer formas rectangulares, la fórmula cambia a la siguiente: (Ax2+Bx2)-4, lo aplicamos con el siguiente ejemplo:
"A" y "B", son el número de plantas por lado pequeño y por lado grande respectivamente, si queremos hacer este rectángulo de 4x6, al aplicar la fórmula obtenemos:
(4x2+6x2)-4= 8+12-4= 16 plantas en total.
Espero que os haya gustado este fácil ejercicio de matemáticas jardineras.
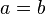
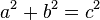
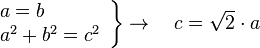
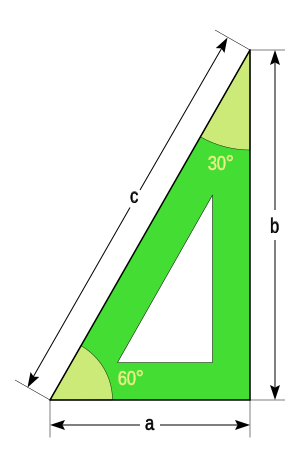

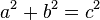
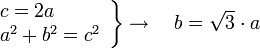
 Si queremos representar un triángulo rectángulo, el más fácil es el Triángulo Egipcio o Triángulo de los 12 nudos, es el nombre moderno dado a un triángulo rectángulo cuyo lados tienen las longitudes 3, 4 y 5, o sus medidas guardan estas proporciones. Es el triángulo rectángulo más fácil de construir y, posiblemente, se utilizó para obtener ángulos rectos en las construcciones arquitectónicas desde la más remota antigüedad.
Si queremos representar un triángulo rectángulo, el más fácil es el Triángulo Egipcio o Triángulo de los 12 nudos, es el nombre moderno dado a un triángulo rectángulo cuyo lados tienen las longitudes 3, 4 y 5, o sus medidas guardan estas proporciones. Es el triángulo rectángulo más fácil de construir y, posiblemente, se utilizó para obtener ángulos rectos en las construcciones arquitectónicas desde la más remota antigüedad.